Saturday, December 17, 2005
44/.44 . I DID IT !!!!!!!!!!!!!!!!!!!!!!!!!!!!
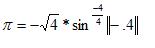
I have finally managed to express all the integers 0 – 100 using only 4 4s (and no other numbers). I’ve sort of been playing with this off and on since 1976, when Mr. C., my math teacher, showed it to the class. I also managed to get ∞ and π
Can anyone get e?
Comments:
<< Home
44/(4-4) is not infinity but undefined. It may seem logical to call it infinity, but that would lead to contradictions. I would think that to get infinity you'd need to use limits.
.
Yes, for infinity I used 44/(4-4) which I say is undefined becaue it is INFINITE! Using limits is not allowed because that would involve using other numbers or i or x or something.
.
For pi, I used -sqrt(4)*(sin^(-4/4))(int(-.4)) which is a lot easier to follow if you look at it in the original posting.
Yes, for infinity I used 44/(4-4) which I say is undefined becaue it is INFINITE! Using limits is not allowed because that would involve using other numbers or i or x or something.
.
For pi, I used -sqrt(4)*(sin^(-4/4))(int(-.4)) which is a lot easier to follow if you look at it in the original posting.
It's not entirely accurate to say that 44/(4-4) is undefined because it is infinite. Afterall, the limit as x approaches 4 of (44/|x-4|)) is infinity. No mathematician will say it is "undefined" simply because it is infinite. So simply being infinite (in the sense that 44/(4-4) is infinite) isn't sufficient grounds for calling an expression undefined.
If you take infinity as the value of a positive real divided by zero, then you end up with contradictions. So while infinity works as the limit of the value of a fraction (with positive constant numerator) as the denominator approaches zero from the right, it does not work as the value of a fraction with the same positive real numerator and a zero denominator.
If you take infinity as the value of a positive real divided by zero, then you end up with contradictions. So while infinity works as the limit of the value of a fraction (with positive constant numerator) as the denominator approaches zero from the right, it does not work as the value of a fraction with the same positive real numerator and a zero denominator.
Oh, and by the way...
When I had Mr. C, and he gave my class the same kind of puzzle (it was to create the numbers using the digits in whatever year it was -- though I forget what year it was), he allowed me to use summations.
I bring that up because summations use a letter (typically i, though I suppose you can use any symbol as long as you don't create ambiguities) as the index of summation. So your reason for rejecting limits would apply to summations as well.
Now I acknowledge the other reason for rejecting limits -- that it makes it too easy to get to any integer (e.g., 5 would be the limit as x goes to 44/44 of x+x+x+x+x). And if you're asking the question, you can set whatever restrictions you want on what can be included in the solutions.
But I still object to the use of 44/(4-4) as infinity, because it is not mathematically correct.
When I had Mr. C, and he gave my class the same kind of puzzle (it was to create the numbers using the digits in whatever year it was -- though I forget what year it was), he allowed me to use summations.
I bring that up because summations use a letter (typically i, though I suppose you can use any symbol as long as you don't create ambiguities) as the index of summation. So your reason for rejecting limits would apply to summations as well.
Now I acknowledge the other reason for rejecting limits -- that it makes it too easy to get to any integer (e.g., 5 would be the limit as x goes to 44/44 of x+x+x+x+x). And if you're asking the question, you can set whatever restrictions you want on what can be included in the solutions.
But I still object to the use of 44/(4-4) as infinity, because it is not mathematically correct.
One more thing about infinity...
Why do you assume that 44/(4-4) is infinity instead of negative infinity?
Why do you assume that 44/(4-4) is infinity instead of negative infinity?
I realize you are joking about just switching the 4s in the denominator. But the humor doesn't get us by the fundamental fact that division by 0 doesn't give you infinity. One demonstration of this is that you don't even get infinity in the limit, because the limit of a ratio (as the denominator approaches 0) doesn't even exist, much less equal infinity. The right limit and the left limit are not equal.
Post a Comment
<< Home



